Unit 18 Set Notation
A Venn diagram is a visual representation of how sets of items (called members or elements) relate to each other.
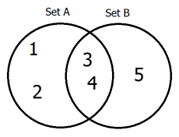
In set notation, each element of a set is listed inside brackets and special symbols are used to evaluate the sets. Sets and set notation are considered mathematical expressions and are transcribed in Nemeth Code, even if the set only contains simple numbers or letters.
Examples:
Set A = {1, 2, 3, 4}
⠠⠎⠑⠞⠀⠠⠁⠀⠨⠅⠀⠨⠷⠂⠠⠀⠆⠠⠀⠒⠠⠀⠲⠨⠾
Set B = {3, 4, 5}
⠠⠎⠑⠞⠀⠠⠃⠀⠨⠅⠀⠨⠷⠒⠠⠀⠲⠠⠀⠢⠨⠾
Note: Examples that are not embedded in UEB have omitted the Nemeth Code switch indicators.
Signs of Operation for Set Notation
| Intersection ∩ | ⠨⠩ |
| Union ∪ | ⠨⠬ |
The intersection of two sets means the elements they have in common.
The union of two sets means the elements of both sets combined.
These symbols are signs of operation and do not require a space on either side of the symbol.
Examples:
A ∩ B = {3, 4}
⠠⠁⠨⠩⠠⠃⠀⠨⠅⠀⠨⠷⠒⠠⠀⠲⠨⠾
A ∪ B = {1, 2, 3, 4, 5}
⠠⠁⠨⠬⠠⠃⠀⠨⠅⠀⠨⠷⠂⠠⠀⠆⠠⠀⠒⠠⠀⠲⠠⠀⠢⠨⠾
Empty Set
When there are no elements in a set, it is called an empty set. This can be written as a set of opening and closing curly brackets with one empty space in between, or the symbol for null.
| No elements - Empty Set { } | ⠨⠷⠀⠨⠾ |
| Null - Empty Set ∅ | ⠸⠴ |
The following examples will evaluate Set B and Set D.
Examples:
B ∪ D = { }
⠠⠃⠨⠬⠠⠙⠀⠨⠅⠀⠨⠷⠀⠨⠾
B ∪ D = ∅
⠠⠃⠨⠬⠠⠙⠀⠨⠅⠀⠸⠴
Signs of Comparison for Set Notation
| Subset of/Includes ⊂ | ⠸⠐⠅ |
| Superset/Contains ⊃ | ⠸⠨⠂ |
| Element of, belongs to ∈ | ⠈⠑ |
| Such That (vertical bar) | ⠳ |
| Therefore ∴ | ⠠⠡ |
SUBSET means "has some elements of" or includes.
SUPERSET means "has all elements of" or contains.
ELEMENT means "belongs to" or member.
SUCH THAT sets a parameter for the set.
THEREFORE is used to express statements.
These symbols are signs of comparison and require a space on either side of the symbol.
Examples:
(Read as: 5 is an element of set B)
5 ∈ B
⠼⠢⠀⠈⠑⠀⠠⠃
(Read as: set C is a subset of set B)
C ⊂ B
⠠⠉⠀⠸⠐⠅⠀⠠⠃
(Read as: set A contains all the members of C)
A ⊃ C
⠠⠁⠀⠸⠨⠂⠀⠠⠉
(Read as: x, such that x is less than 5)
{x | x<5}
⠨⠷⠭⠀⠳⠀⠭⠀⠐⠅⠀⠢⠨⠾
(Read as: a equals b, therefore, b equals a)
a = b ∴ b = a
⠁⠀⠨⠅⠀⠃⠀⠠⠡⠀⠃⠀⠨⠅⠀⠁
Find x if; x = {red, blue, pink}
⠠⠋⠔⠙⠀⠰⠭⠀⠊⠋⠆⠀⠸⠩⠀⠭⠀⠨⠅⠀⠨⠷⠗⠑⠙⠠⠀⠃⠇⠥⠑⠠⠀⠏⠊⠝⠅⠨⠾⠀⠸⠱
* Notice that this example is written with Nemeth Code switching.
Negation
The symbol for negation can be used to express "not" in front of a symbol of comparison.
Examples:
(Read as: 4 is not an element of set A)
4 ∉ A
⠼⠲⠀⠌⠈⠑⠀⠠⠁
(Read as: X is not a subset set Y)
X ⊄ Y
⠠⠭⠀⠌⠸⠐⠅⠀⠠⠽
Brain Boost
Enclosed Lists
In Nemeth Code, when a set contains only values, such as numbers, letters, or math expressions, the list can be enclosed in grouping signs without having to use numeric or letter indicators.
Nemeth Code Definition: An enclosed list must contain two or more numbers, letters, math expressions, or sign of omission enclosed in grouping signs (usually curly brackets) and separated by mathematical commas. The list cannot contain any other sign of punctuation, any word, abbreviation, number with ordinal or plural end, or sign of comparison. Enclosed lists are considered mathematical expressions, even if they contain only letters, and are transcribed in Nemeth Code. No numeric indicator is used before a numeral or decimal point, and no ELI is used before a letter or roman numeral in regular type. Long dash and ellipsis may be used for omissions, and the shape indicator may be included.
Examples:
A = {2, 4, 6, …, 10}
⠠⠁⠀⠨⠅⠀⠨⠷⠆⠠⠀⠲⠠⠀⠖⠠⠀⠄⠄⠄⠠⠀⠂⠴⠨⠾
{2+2, 2+3, 2+4}
⠨⠷⠆⠬⠆⠠⠀⠆⠬⠒⠠⠀⠆⠬⠲⠨⠾
{1, a, 2, b, 3, c}
⠨⠷⠂⠠⠀⠁⠠⠀⠆⠠⠀⠃⠠⠀⠒⠠⠀⠉⠨⠾
X = (-1, 0, 1, 2)
⠠⠭⠀⠨⠅⠀⠷⠤⠂⠠⠀⠴⠠⠀⠂⠠⠀⠆⠾
[.011, .11, 1.1, 11]
⠈⠷⠨⠴⠂⠂⠠⠀⠨⠂⠂⠠⠀⠂⠨⠂⠠⠀⠂⠂⠈⠾
{i, ii, iii, iv, v}
⠨⠷⠊⠠⠀⠊⠊⠠⠀⠊⠊⠊⠠⠀⠊⠧⠠⠀⠧⠨⠾
{∠ d, ∠ e, ∠ f}
⠨⠷⠫⠪⠀⠙⠠⠀⠫⠪⠀⠑⠠⠀⠫⠪⠀⠋⠨⠾
An enclosed list should not be divided between braille lines. If there is not enough space on a line, the entire enclosed list must be brought down to the next line.
